|
The scale-widths obtained from the velocity data agree quite well
with estimates of the local radius of deformation computed from
hydrographic profiles taken just outside the stream to either side,
Figure 9 (below).
|
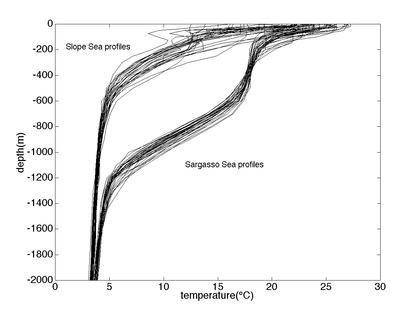
|
|
Figure 9. Temperature profiles from 30 hydrographic stations to either
side of the Gulf Stream in the immediate vicinity of the Oleander
line. These and the corresponding salts were used to calculate the
radius of deformation.
|
|
To see this we use linear theory for planetary wave motion
in a stratified ocean. Essentially, we look for the lowest eigenvalue
(i=1) for the equation:
|
|
d2w/dz2 + ci2N2w=0
|
|
where N is the Brunt-Vailala frequency, ci are the eigenvalues, and
the subscript i refers to mode number. The radius of deformation =
1/cif in meters where f = Coriolis parameter =
0.9x10-4s-1 for this
region of the Gulf Stream.
|
|
Using a set of 30 hydrographic stations
near the Oleander line just north and south of the Gulf Stream we
obtain 19.7 and 34.3 km respectively.
|
|
These values agree well with
estimates made for larger 4° by 4° regions in the vicinity of the Gulf
Stream (Emery et al., 1984).
|
|
These values also agree quite well
with the scale-widths for the mean velocity shear determined from
the stream-coordinate mean (Figure 2).
|



