Appendix B: Lagrangian Statistics

A Lagrangian description of motion is based upon the trajectories of individual particles. Consequently, statistics based on this approach are defined over time series of individual drifter observations. The kernel of all such statistics is the Lagrangian autocovariance function. Through Taylor's (1921) theory of homogeneous turbulence, this function can be related to the steady-state single particle eddy diffusivity and in turn to the Lagrangian integral time and length scales.

Let the Lagrangian velocity and displacement at time t of a particle passing through location x at time t₀ be denoted by v(t|x,t₀) and r(t|x,t₀), respectively. Let the Lagrangian operator <>_L signify an average taken over an ensemble of particles released randomly from x. Then we can define the Lagrangian mean velocity and Lagrangian mean displacement at time t₀ + t of an ensemble of particles released from x at time t₀ by

Finally, we denote the residual velocity and displacement about these means as and , respectively.

The Lagrangian autocovariance function is defined (Davis, 1991) as

where t is the time lag of interest, and where the subscripts i and j may take the values 1 for the zonal direction or 2 for the meridional direction. Davis (1991) further defines the single particle eddy diffusivity as

The four components are also frequently written in tensor notation:

Taylor (1921) showed that for homogeneous (location independent) and stationary (time independent) turbulence fields, the time lag dependence of disappears eventually, as the diffusion becomes a random-walk (Colin de Verdière, 1983), leaving

where T represents the time at which the random walk begins. At time lags in excess of T, the diagonal elements of are simply the products of the respective velocity variances and integral time scales (Freeland et al., 1975). Equivalently,

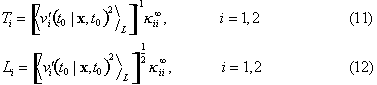
give the Lagrangian time and length scales (Poulain et al., 1996) in terms of the steady-state diffusivity.

The Lagrangian statistics, , T_i and L_i, were estimated from real and numerical drifters in the following way. First, the Eulerian mean flow was removed from the drifter velocities to minimize the contribution of deterministic horizontal shear to dispersion (Poulain, 2001). For the real drifters, the 2° x 2° mean flow was interpolated at the drifter locations using cubic splines. For the numerical drifters, the Eulerian mean flow, i.e., the non-masked average of the model velocities at each grid point for the 5-year period, was interpolated to the drifter location and was removed from the drifter velocity.

By definition Lagrangian velocity statistics should be computed over an ensemble of selected particles. This is not practically feasible using one single realization of real or numerical drifters and the assumptions of stationarity and uniformity (at least locally) were used to estimate statistics that characterize the displacement and absolute dispersion of selected drifters over time. Domain of 5° x 5° size were chosen as a good compromise to resolve the spatial variations of the Lagrangian statistics while maintaining a relatively large amount of observations to assure the robustness of the statistics. Assuming stationarity and uniformity of the statistics within 5° x 5° bins, each daily drifter observation in the domain was considered as a "deployment" position from which the drifter is tracked with positive time lags (arriving at the position) and with negative time lags (going away from that position). Likewise, the Lagrangian statistics defined in (5), (6), (7) and (8) were estimated for particles reaching (positive time lags) and leaving (negative time lags) the spatial domain considered (Davis, 1991; Poulain et al., 1996). The lag-independent diffusivities defined in (10) and the corresponding time and length scales (11-12) were practically estimated from the maximal values of in the 0-25 day time lag range.

Lagrangian statistics depend not only upon the spatial domain selected but also on the time lag. For turbulent motions, however, they plateau after time lags of the order of the integral time scale, for both positive and negative time lags; the covariances approach zero and the diffusivities (diagonal elements) and scales asymptote to maximum constant values (Taylor, 1921). Since Lagrangian statistics are intrinsically non-local as particles spread over a finite-size domain they can include dispersion effects by the mean flow shear. Removing the Eulerian mean flow from the drifter velocities before computing Lagrangian statistics eliminates partially this problem except in regions of high horizontal shear such as in the vicinity of the Gulf Stream.